5. Переоценка вертикальных линий

Очевидно, в силу исторически накопленного опыта, с одной стороны, и благодаря расположению линии, соединяющей глаза человека в горизонтальной плоскости, с другой, человек обладает способностью точнее определить на глаз горизонтальные расстояния, чем высоту предметов. Оказывается, острота зрения "в горизонтальном направлении" больше, чем в вертикальном, а глазомерное сравнение длины параллельных горизонтальных линий может быть произведено с точностью до 1%, тогда как для вертикальных такая точность недостижима. Поворот глаза в вертикальной плоскости требует большего мышечного напряжения, чем аналогичный поворот в горизонтальной плоскости, а так как мышечное напряжение может выступать как мерило пути, то вертикальные расстояния кажутся нам больше равных им горизонтальных. Поэтому большинство людей обладает способностью преувеличивать вертикальные протяженности по сравнению с горизонтальными, и это также приводит к иллюзиям зрения. Вот несколько примеров этих иллюзий (рис. 53-58).

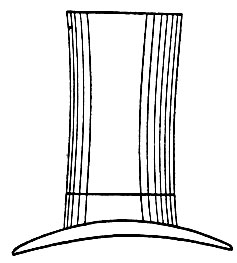
Рис. 53. Высота шляпы-цилиндра кажется больше, чем ширина полей, хотя они равны

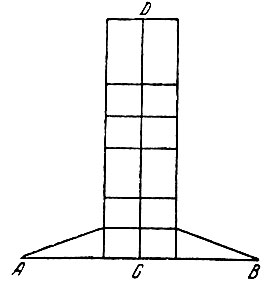
Рис. 54. Высота CD фигуры кажется больше ее основания АВ, хотя AB=CD

Рис. 55. Высота черной гребенки кажется больше ее ширины, хотя они равны. Поворотом фигуры набок легко добиться исчезновения иллюзии

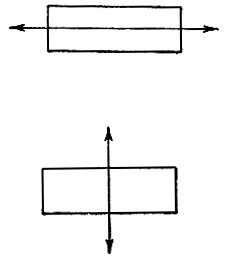
Рис. 56. Нижний прямоугольник кажется короче и толще верхнего, хотя эти фигуры равны

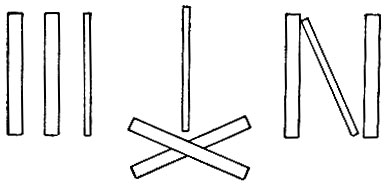
Рис. 57. Три вертикальные полоски слева имеют одинаковую высоту, но если их расположить, как показано в центре рисунка, или так, как показано справа, то узкая полоска кажется длиннее двух широких

Рис. 58. Верхние части типографских знаков кажутся равными по высоте нижним, хотя они на самом деле меньше нижних, в чем можно убедиться, перевернув рисунок

Если предложить ряду лиц начертить вертикальную и горизонтальную линии одинаковой длины, то в большинстве случаев начерченные вертикальные линии будут короче горизонтальных. При делении на глаз вертикальной линии пополам обычно середина оказывается слишком высоко (см. рис. 40).

Вертикальные параллельные линии при значительной их длине кажутся обычно в верхней части слегка расходящимися. Заметим, что горизонтальные кажутся всегда сходящимися. Это обстоятельство учитывается, между прочим, в архитектуре, где высокие колонны, для того чтобы они казались нам правильно параллельными, делаются вверху слегка сходящимися. Так, например, построена колоннада Парфенона в Греции.

Заметим, что вследствие преувеличения вертикальных линий в архитектуре приходится считаться еще и с таким обстоятельством. Если глаз фиксирует горизонтальную прямую, находящуюся на одном уровне, то выше лежащие прямые кажутся искривленными. Для устранения этого кажущегося архитектурного недостатка приходится принимать соответствующие меры.

К рассматриваемой группе иллюзий близко примыкают иллюзии заполненного пространства (рис. 59-61). Заполненное пространство, по которому глаз скользит горизонтально, удлиняется. Так, например, на море все расстояния кажутся меньшими, так как беспредельный простор моря является пространством неподразделенным. Здания, украшенные фигурами и орнаментами, кажутся нам больше своей действительной величины.

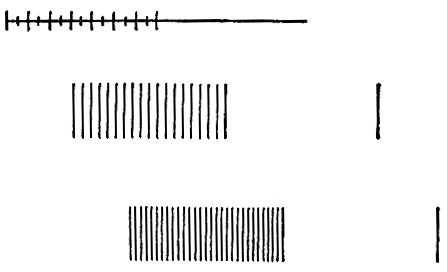
Рис. 59. Заполненное пространство кажется длиннее незаполненного

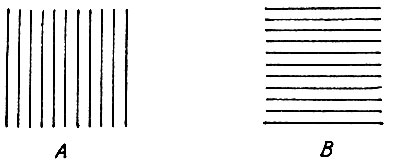
Рис. 60. Правый заштрихованный квадрат кажется уже и выше левого.

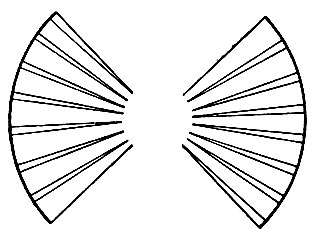
Рис. 61. Заштрихованные секторы кажутся меньше незаштрихованных. На самом деле это равные квадранты одного и того же круга. Наш взгляд невольно скользит к центру круга и легче перемещается по горизонтали, чем по вертикали (в силу привычки)

На рис. 60 нам кажется, что правая фигура В уже и выше (взгляд скользит по вертикали) левой фигуры А. На самом деле и А и В - правильные заштрихованные квадраты.

Значит, заполненное пространство нам кажется всегда шире незаполненного и по горизонтали и по вертикали? Однако это не всегда так, и многое зависит от направления, по которому скользит наш взгляд, стремясь воспринять фигуру (рис. 61).

Возможны, между прочим, случаи неправильного восприятия и сравнения горизонтальных линий (рис. 62).

Рис. 62. Иллюзия трубки. Левые черточки кажутся более длинными, чем правые, хотя те и другие имеют одинаковую длину. Точно так же площадь правой фигуры кажется большей, хотя ясно, что площади равны